

최근의 높은 성능을 기록하는 딥러닝 모델들은 모델의 크기가 굉장히 크다. 이에 다양한 경량화 방법론이 등장했다. Pruning과 distillation 같은 압축 방법론들은 모델의 파라미터 숫자를 줄인다. 하지만 그에 비해 Quantization은 파라미터의 bits 개수를 줄인다. Quantization의 경우는 이미 잘 갖춰진 모델의 아키텍쳐를 바꾸지 않기 때문에 필연적으로 weight 자체를 제거하고 줄이는 distillation이나 pruning에 비해 성능 손실이 거의 없이 모델을 경량화 할 수 있다.
기학습된 모델에 Scalar Quantiztion과 같은 방법을 적용하는 것은 좋은 압축률을 보이지만 오류가 누적되면 큰 성능 하락을 일으킬 수 있다. 이 문제를 해결하기 위해 학습 중에도 Quantization을 적용하고자 했지만 그랬을 때 문제는 대부분의 이산화(discretization) 연산은 Gradient가 없다는 점이다. 대부분 미분했을 때 0이 된다.
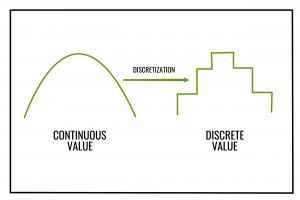
간단히 생각해보면 원래 값이 어떤 실수x라고 했을 때, 이 숫자를 1bit로 discretization한다고 생각해보자. x가 0보다 크면 1, 아니면 0이다. 그러면 이 함수의 그래프를 그려보면
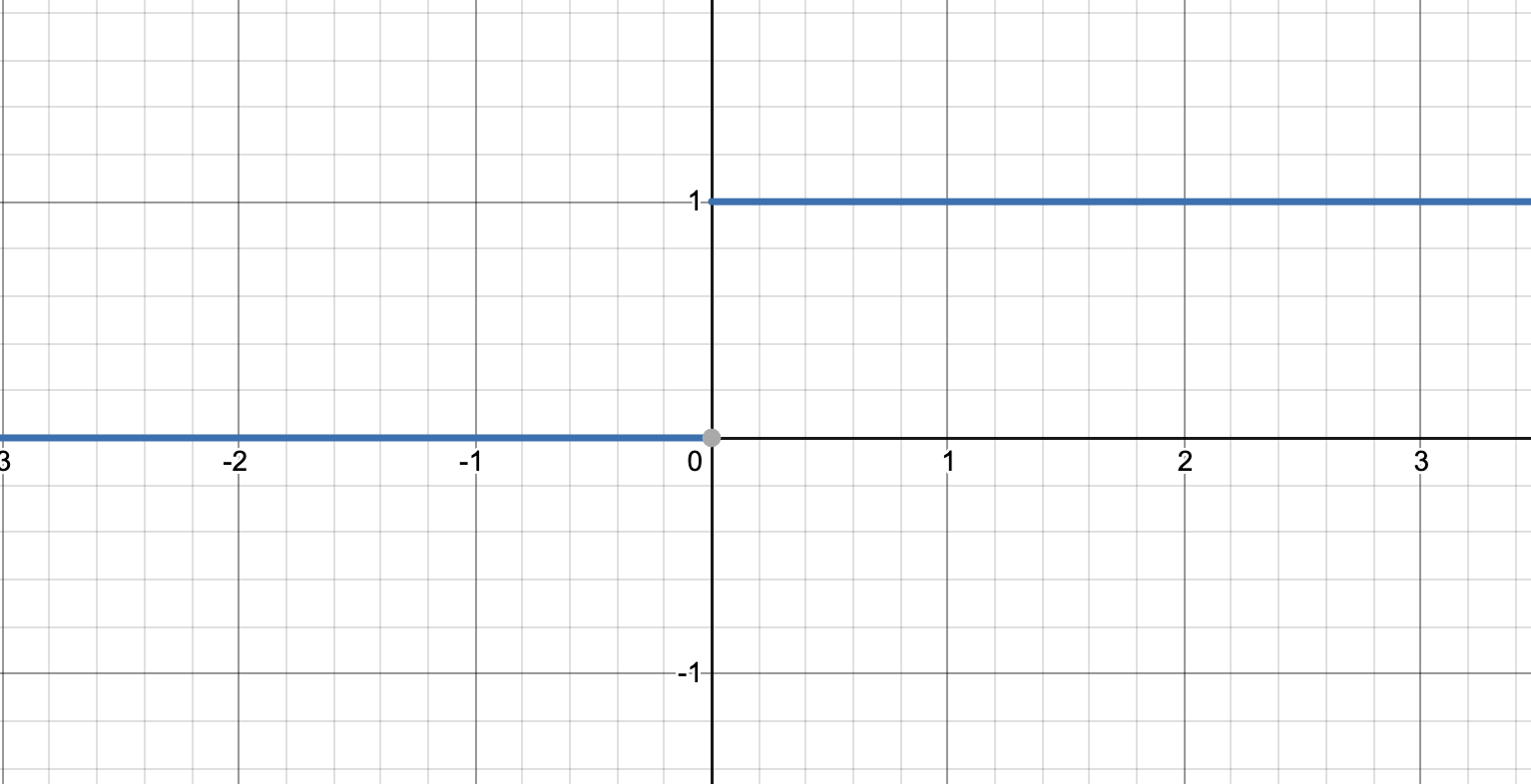
이런 모양이 된다. 여기서 고등수학을 배운 사람들이라면 이 함수의 x대한 미분값은 그래프의 기울기라는 것을 알 것이다. 기울기는 모든 곳에서 0이다. 본질적으로 이산화 연산은 어쨌든 연속 공간에 있는 값을 특정한 몇 개로 줄이는 연산이기 때문에 gradient가 거의 0이 되는 것이다.
그래서 이를 해결하기 위해서 Quantization Aware Training(QAT)은 Straight Through Estimator(STE)를 이용해서 gradient를 계산한다. 히지만 이 방법은 STE에 의한 에러가 작을 때 사용할 수 있다.

그림 a)는 일반적인 Quantization방법이고, 그림 b)는 QAT이다.
일반적인 Quantization은 모델이 training이 다 끝난 후에 Quantization을 진행하게 된다. 반면에, QAT는 일반적인 모델 설계단계와 동일하게 weight을 initialize 해주고, 이 weight에 대해 quantization을 진행하게 된다. 그 후 model을 거쳐서 나온 output에 대해서도 quantization을 진행하여 최종적인 output을 계산하게 되는 것이다. 즉, 일반적인 quantization은 training이 다 끝난 후 quantization을 적용하는 것이고, QAT는 training과정 중에 지속적으로 quantization을 적용하는 것이다.
그럼 QAT과정 중에 weight, biases들은 어떻게 update 하는 것일까?여기서 필요한 개념이 STE이다. 이는 gradient가 흐를 수 있게 하는 것으로, quantization 전의 gradient와 후의 gradient를 항등 함수로 처리하겠다는 것이다. 즉, Relu를 거쳐 나온 output을 u, u에 대해 quantization을 적용 한 값을 v라고 하면, $\frac{∂u}{∂L}=\frac{∂v}{∂L}$로 계산하여, gradient가 null이 되는 상황을 막아준다.
논문의 핵심적인 방법은 Quant-Noise라고 부르는 Noise를 모델 전체가 아닌 모델의 일부 weight에 적용해 학습을 진행하는 것이다. 그렇게 했을 때 STE를 사용하고 모델 전체를 Quantization했을 때와 달리 noise가 추가되지 않은 weight는 정상적으로 계산된 gradient로 학습을 할 수 있기 때문에 훨씬 안정된 성능을 얻을 수 있다.
저자들이 말하는 자신들의 기여는 다음과 같다.